Selesaikan linier, kuadrat, kerucut, bilangan bulat, dan nonlinier
masalah optimasi
Kotak Alat Pengoptimalan menyediakan fungsi untuk menemukan parameter yang meminimalkan atau memaksimalkan tujuan sekaligus memenuhi batasan. Toolbox ini mencakup pemecah untuk pemrograman linier (LP), pemrograman linier bilangan bulat campuran (MILP), pemrograman kuadrat (QP), pemrograman kerucut orde kedua (SOCP), pemrograman nonlinier (NLP), kuadrat terkecil linier terbatas, kuadrat terkecil nonlinier, dan persamaan nonlinier.
Anda dapat menentukan masalah optimasi dengan fungsi dan matriks atau dengan menentukan ekspresi variabel yang mencerminkan matematika yang mendasarinya. Anda dapat menggunakan diferensiasi otomatis fungsi tujuan dan batasan untuk solusi yang lebih cepat dan akurat.
Anda dapat menggunakan pemecah toolbox untuk menemukan solusi optimal terhadap masalah yang berkesinambungan dan terpisah, melakukan analisis trade-off, dan menggabungkan metode optimasi ke dalam algoritma dan aplikasi. Toolbox memungkinkan Anda melakukan tugas pengoptimalan desain, termasuk estimasi parameter, pemilihan komponen, dan penyetelan parameter. Ini memungkinkan Anda menemukan solusi optimal dalam aplikasi seperti optimalisasi portofolio, manajemen dan perdagangan energi, serta perencanaan produksi.

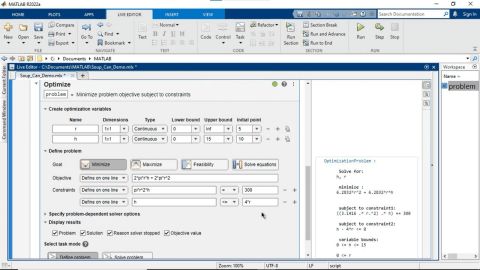
Memodelkan masalah desain atau keputusan sebagai masalah optimasi. Tetapkan parameter desain dan keputusan sebagai variabel pengoptimalan. Gunakan variabel untuk menentukan fungsi tujuan untuk mengoptimalkan dan menggunakan batasan untuk membatasi kemungkinan nilai variabel.
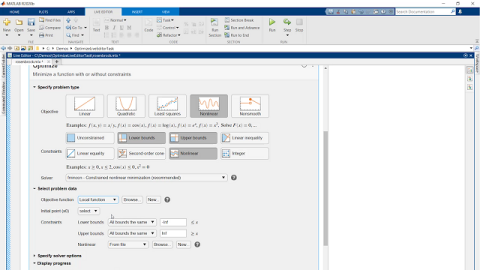
Menerapkan pemecah masalah optimasi untuk menemukan solusi optimal: sekumpulan nilai variabel optimasi yang menghasilkan nilai optimal dari fungsi tujuan, jika ada, dan memenuhi batasan, jika ada.

Memecahkan masalah optimasi yang memiliki tujuan nonlinier atau memiliki batasan nonlinier.
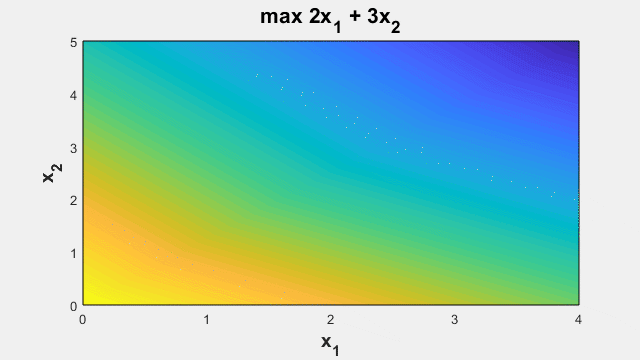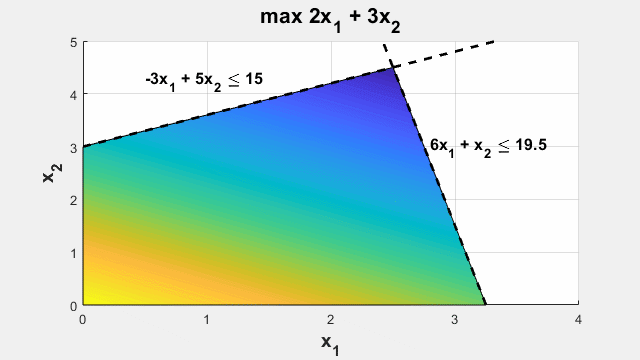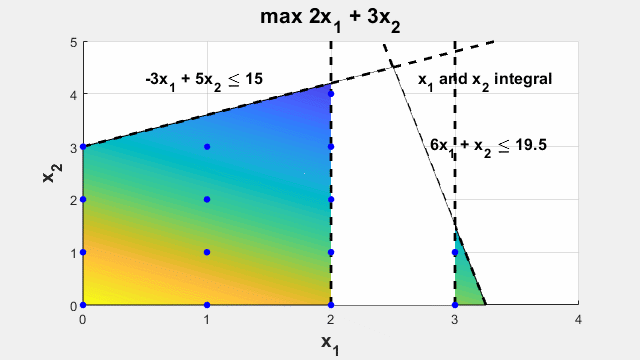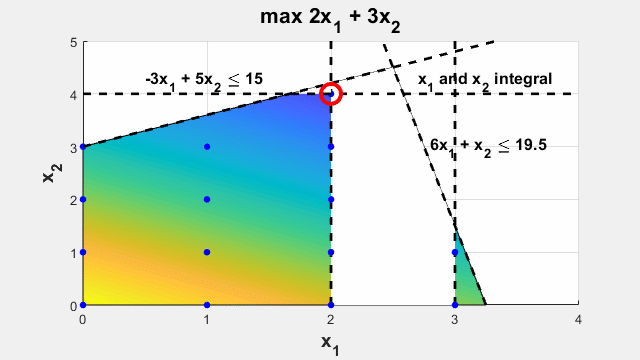
Menyelesaikan masalah optimasi yang memiliki tujuan linier yang tunduk pada batasan linier dengan variabel kontinu dan/atau bilangan bulat.
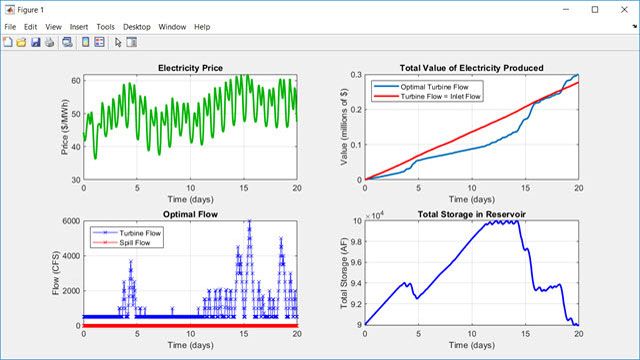
Menyelesaikan masalah optimasi dengan batasan objektif kuadrat dan linier atau masalah dengan batasan kerucut orde kedua.
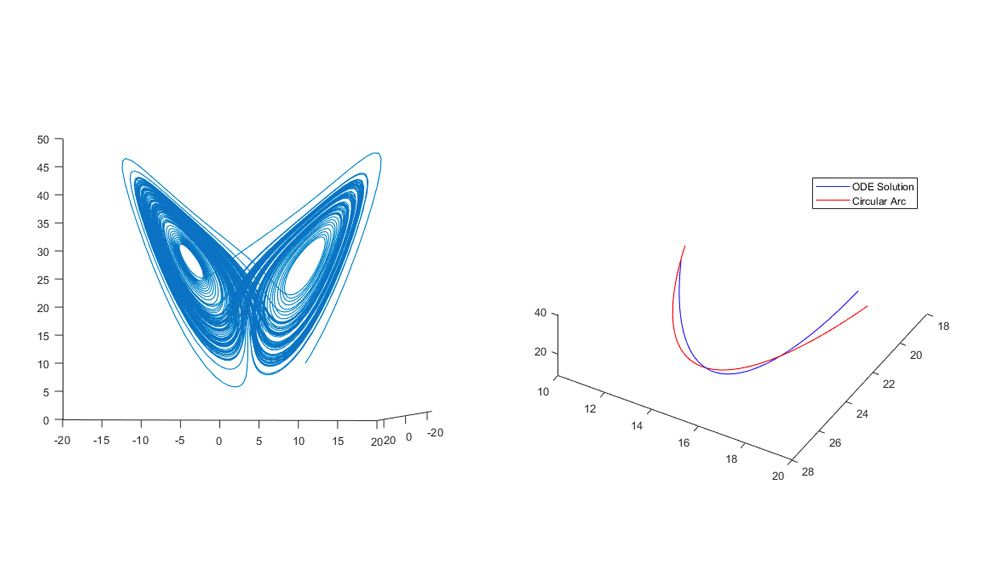
Solve linear and nonlinear least-squares problems subject to bound, linear, and nonlinear constraints.
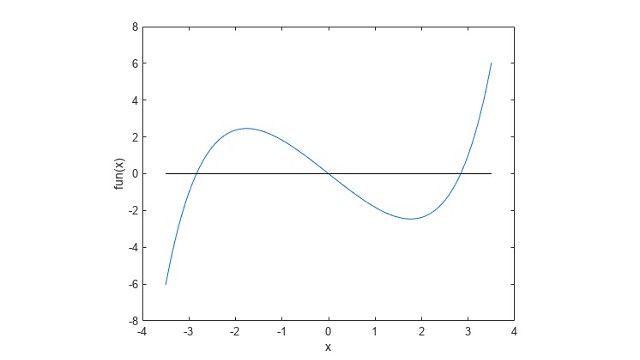
Memecahkan sistem persamaan nonlinier yang tunduk pada batasan terikat, linier, dan nonlinier.
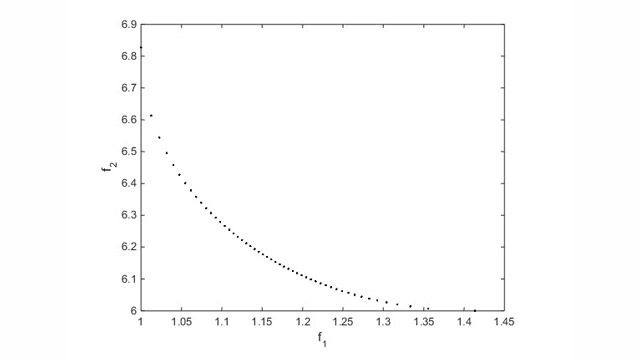
Memecahkan masalah optimasi yang memiliki banyak fungsi tujuan yang tunduk pada serangkaian batasan.
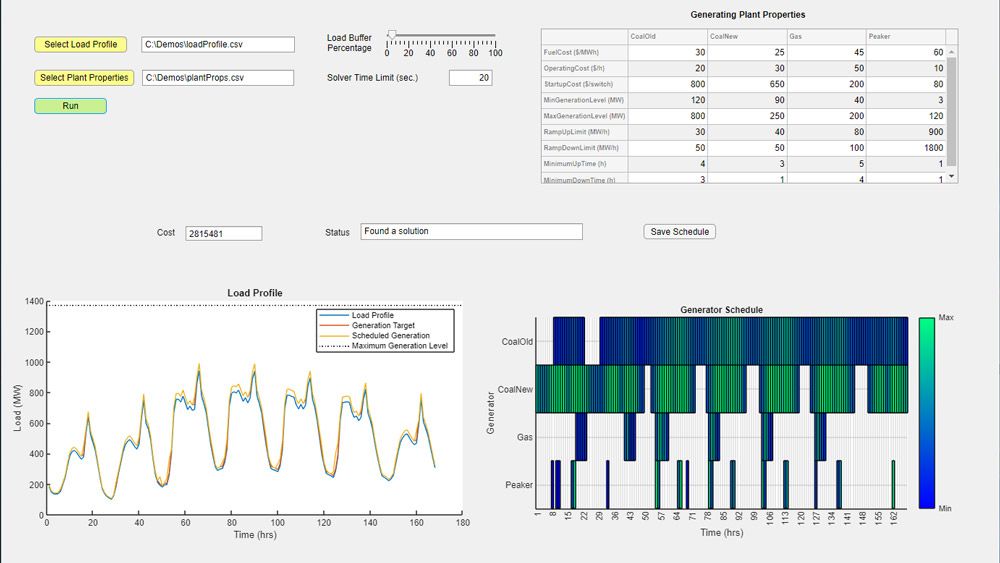
Membangun dukungan keputusan dan alat desain berbasis pengoptimalan, berintegrasi dengan sistem perusahaan, dan menerapkan algoritme pengoptimalan ke sistem tertanam.
“MATLAB telah membantu mempercepat R&D dan penerapan kami dengan algoritme numerik yang kuat, alat visualisasi dan analitik yang ekstensif, rutinitas pengoptimalan yang andal, dukungan untuk pemrograman berorientasi objek, dan kemampuan untuk berjalan di cloud dengan aplikasi Java produksi kami.”
Borislav Savkovic, buildingIQ

Eksplor 30 Hari Gratis
Dapatkan informasi harga dan jelajahi produk terkait.
Sekolah Anda mungkin sudah menyediakan akses ke MATLAB, Simulink, dan produk tambahan melalui lisensi seluruh kampus.
TUTORIAL
Onramp Pembelajaran Mendalam
SUMBER DAYA
Tutorial dan Contoh Pembelajaran Mendalam
BUKU GRATIS
Panduan Praktis untuk Pembelajaran Mendalam: Dari Data hingga Penerapan

AKR Tower – 9th Floor
Jl. Panjang no. 5, Kebon Jeruk
Jakarta Barat 11530 – Indonesia